PROSTI BROJEVI I FAKTORIZACIJA
Ovaj problem se često javlja u rešavanju nekih složenijih zadataka.
Jedan od mogućih algoritama za rešenje:
Posle učitanih brojeva a i b prolazi se redom kroz sve brojeve na ovom intervalu koristeći for ciklus.
Za svaki od tih brojeva proverava se da li je prost i ako jeste ispisuje se.
Provera da li je broj prost(metoda):
Ako je 1 ili 2 broj je prost. Ako nije uvedemo bool promenljivu koja se u početku postavi na true. To znači da pretpostavljamo da će broj biti prost. Kroz ciklus menjamo delioc počev od dva pa sve dok ne naiđemo na onaj, sa kojim će ispitivani broj biti deljiv. Kad naiđemo na takav, prekidamo ciklus. Ako je poslednji delioc manji od ispitivanog broja, onda znači da broj nije prost, jer je deljiv sa još nekim brojem osim sa jedinicom i sa samim sobom(definicija prostih brojeva).
U tom slučaju bool promenljivu treba promeniti na false.
Dakle povratna vrednost metode će biti true, ako je broj prost ili false ako nije.
{
long long a,b,c=0;
cin >> a >> b;
for(int i=a;i<=b;i++){
if(isProst(i)){
cout << i << " ";
c++;
if(c%10==0)cout << endl;
}
}
return 0;
}
#include < iostream >
using namespace std ;
bool isProst(long long b){
if(b==1 || b==2)
return true;// 1 i 2 su prosti brojevi
bool r=true;
long d=2;
/* Trazi broj koji je delilac broja b na segmentu od 2 do b*/
while(b % d != 0 )// Uslov petlje je da b nije deljiv sa d
{
d++;
}
if(d < b)
r=false;
return r;
}
int main(){
long long a, b ,c=0;
for(int i=a; i <= b; i++)
{
if(isProst(i))
{
cout << i << " ";
c++;
if(c % 10 == 0)
cout << endl;
}
}
}
Postoji način da se određivanje da li je broj prost ubrza, što je objašnjeno dalje u tekstu.
Svođenje broja iteracija sa n na √n
Ako malo bolje analiziramo delioce nekog broja možemo uočiti da ako je d delioc nekog broja n i n/d će takođe biti delioc tog istog broja. Npr. broj 6 je delioc broja 42, ali takođe je i broj 7=42/6. Može se dalje uočiti da bar jedan od ova dva delioca mora biti manji ili jednaki od √n. U slučaju da su oba delioca jednaka, broj n je njihov potpun kvadrat, a vrednost oba delioca je tačno jednaka √n
Na osnovu ovog možemo zaključiti da je potreban broj provera da li je broj n prost najviše jednak √n
#include < iostream >
using namespace std ;
bool isProst(long long n)
{
if(n==1)
return false;
long long d=2;
while(d*d<=n){
if(n % d == 0)
{
return false;
}
d=d+1;
}
return true;
}
int main()
{
long long a, b ,c=0;
for(int i=a; i <= b; i++)
{
if(isProst(i))
{
cout << i << " ";
c++;
if(c % 10 == 0)
cout << endl;
}
}
}
Algoritam ispitivanje da li je broj prost koristeći 6k+1 teoremu
#include < iostream >
using namespace std ;
bool isProst(long long b)
{
if(n==1)
return false;
if(n==2 || n==3)
return true;
long long k=1;
while((6*k-1)*(6*k-1)<=n)
{
if(n % (6*k-1) == 0 || n % (6*k+1) == 0)//Ispituje samo oblike 6k+1 i 6k-1, k=1,2,3...
{
return false;
}
k=k+1;
}
return true;
}
int main()
{
long long a, b ,c=0;
for(int i=a; i <= b; i++)
{
if(isProst(i))
{
cout << i << " ";
c++;
if(c % 10 == 0)
cout << endl;
}
}
}
Određivanje svih delioca nekog broja
Delioci broja 12: 1,2,3,4,6,12
Faktorizacija bi bila da napišemo proizvod delilaca koji bi dali broj n. Za n=12, faktorizacija bi značila:
12=1*2*2*3
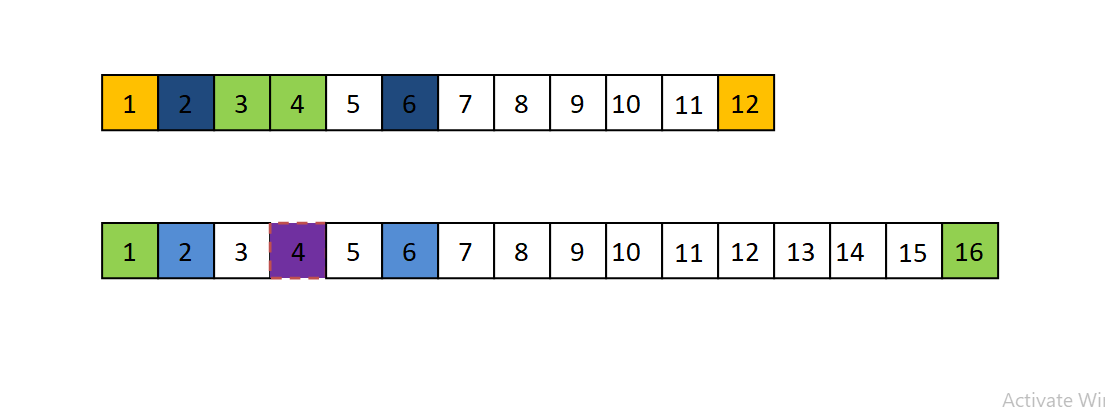
Kod određivanja delioca, kao i kod određivanja prostih brojeva, važi zaključak da je dovoljno ispitati brojeve maksimalno do vrednosti n ^1/2. Svaki delioc d ima svog para n/d. Ovo se vodi na slici 1. Na primer delioci broja 12: 1 i 12, 2 i 6, 3 i 4. Delioci broja 16 su: 1 i 16, 2 i 8, 4 i 4. Dakle ovde vidimo da je 4 u paru sa samim sobom i da je 4=16^1/2.
#include < iostream >
#define DIM 100
using namespace std ;
int d[DIM];
long long sviDelioci(long long n)
{
long long m=0;
long long i=1;
while(i*i < n)
{
if(n % i == 0)
{
d[m+1]=i;
d[m+2]=n/i;
m=m+2;
}
i=i+1;
}
if(i*i == n)
{
m=m+1;
d[m]=i;
}
return m;
}
int main()
{
long long N,m;
cin >> N;
m=sviDelioci(N);
for(int i=1;i<=m;i++){
cout << d[i] << endl;
}
}
Faktorizacija broja N
{
{
d[m+2]=n/i;
m=m+2;
i=i+1;
if(i*i == n)
{
d[m]=i;
#include < iostream >
#define DIM 100
using namespace std ;
int a[DIM];
int p[DIM];
int faktorizacija(int n)
{
int k=0;
int d=2;
while (d*d<=n) {
if(n % d == 0){
k=k+1;
a[k]=0;//Izlozilac koji se pamti u nizu
p[k]=d;
while(n % d==0){
n=n/d;
a[k]=a[k]+1;
}
}
d=d+1;
}
if(n>1){
k=k+1;
p[k]=n;
a[k]=1;
}
return k;
}
int main()
{
int N,k;
cin << N;
k=faktorizacija(N);
for(int i=1; i<=k; i++)
{
for(int j=1; j<=a[i]; j++) {
cout << p[i] << endl;
}
}
}
|
Sledeće
Eratostenovo sito >| |