REKURZIVNI ALGORITMI
Dati problem koji je složen se prvo podeli na više manjih problema, koje je lakše rešiti.Svaki taj potproblem se rešava nezavisno jedan od drugog i kada se svaki od nih reši, onda se ta rešenja kombinuju in a taj način rešava složen problem, od koga se pošlo.
Za razliku od petlji gde se određen postupak koji se ponavlja navodi u telu petlje, rekurzivni postupak je takođe iterativan, ali postupak koji se ponavlja je sam algoritam koji sam sebe poziva više puta direktno ili indirektno pozivanjem neke naredbe ili funkcije, koja onda poziva dati algoritam(funkciju).
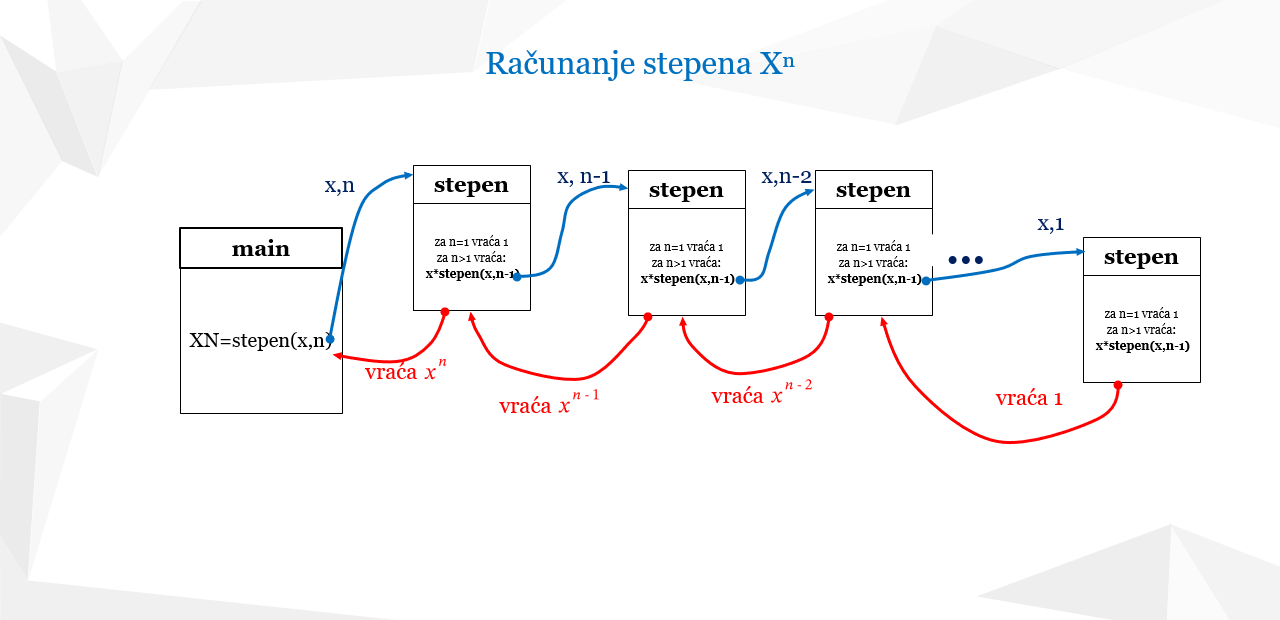
Rekurzija primer: Izračunavanje stepena Xn
Xn=X*X*X* … *X= X*Xn-1 * X
Rešenje pomoću petlje
for(int i=0; i
printf("XN=%d\n",XN);
Rešenje pomoću rekurzije
Xn = Xn-1 * X
X0 = 1
Kod koji ovo rešava:
C
int stepen(int x, int n)
{
int main() {
scanf("%d%d",&X,&N);
XN=stepen(X,N);//Poziv funkcije za računanje stepena
printf("%d\n" ,XN);
return 0;
C++
using namespace std;
int stepen(int x, int n)
{
int main() {
cin >> X;
cin >> N;
XN=stepen(X,N);
cout << XN << endl;
return 0;
Fibonačijev niz
|
Zadatak kojim se određuje n-ti član Fibonačijevog niza, može se između ostalog rešiti rekurzijom: Pogledajte više o tome na strani:
Fibonačijev niz |
Iz decimalnog zapisa u binarni
Primer 1:
Ulaz
22
Izlaz
0000 0000 0001 0110
Primer 2:
Ulaz
2147483647
Izlaz
1111 1111 1111 1111
21=2
22=4
23=8
24=16
25=32
....
|
S obzirom da se radi o int podacima koji imaju 16 bitova memorije, vrednost na krajnjoj levoj poziciji iznosi:
|
215
|
|
215 = 32768
|
Svaki sledeći je duplo manji. Rekurzija se završava kada ovaj broj dostigne 1.
|
Rešenje u programskom jeziku C
#include < math.h >
/* rekurzivna funkcija koja pretvara iz decimalnog u binarni zapis .
parametri: n-broj u dekadnom zapisu, s2- stepen broja 2 */
void db(int n,int s2)
{
{
t = (n >= s2)? n-s2 : n;/* Ako je stepen broja dva(s2) manji od broja u dekadnom zapisu onda se kao ostatak(t) uyima vrednost razlike (n-s2), u suprotnom t=n*/
db(t,s2/2);/* poziv rekurzivne funkcije za pretvaranje dekadnog u binarni zapis */
int main()
{
scanf("%d",&n);
/*izlozilac broja 2 */
while(i < 15){
s2 *= 2;
db(n,s2);/*poziv rekurzivne funkcije za pretvaranje dekadnog u binarni zapis */
return 0;
Rešenje u programskom jeziku C++
using namespace std;
/* rekurzivna funkcija koja pretvara iz decimalnog u binarni zapis .
parametri: n-broj u dekadnom zapisu, s2- stepen broja 2 */
void db(int n, int s2)
{
{
t = (n >= s2)? n-s2 : n;
db(t,s2/2);/* poziv rekurzivne funkcije za pretvaranje dekadnog u binarni zapis */
int main()
{
cin >> n;
/*izlozilac broja 2 */
while(i < 15) {
s2 *= 2;
db(n,s2);/* poziv rekurzivne funkcije za pretvaranje dekadnog u binarni zapis */
return 0;
Računanje determinante kvadratne matrice dimenzije n
Učitati dimenziju "n" matrice A , a zatim učitati matricu. Kreirati aplikaciju koja rešava determinantu matrice D(A) i ispisuje na ekranu.
Matricu ćemo definisati upotrebom pokazivača kao dvodimenzionalni dinamički niz (int ** A). Više o dinamičkim dvodimenzionalnim nizovima-matricama, kako se definišu, učitavaju, ispisuju, kopiraju itd. pročitajte u članku: Dvodimenzioni dinamički nizovi-matrice.
Kod prikazan u nastavku je detaljno objašnjen u pomenutom članku, a ovde će biti samo prikazan:
#include < stdlib.h >
#include< math.h >
/*Funkcija za ispisivanje matrice
* parametri su
* a- pokazivač na matricu(pokazivač na pokazivač)
* n -dimenzija matrice
*/
void ispisatiMatricu( int ** a, int n)
{
{
{
printf("\n");
int main()
{
int **A;
printf("n=?\n");
scanf("%d",&n);
A=(int**)malloc(n*sizeof(int*));
printf("Matrica?\n");
for(int i=0; i < n; i++)
{
for(int j=0; j < n; j++)
{
printf("Matrica ispis:\n");
ispisatiMatricu(A,n);
return 0;
Ove parametre je potrebno pripremiti u main funkciji, pre poziva funkcije za rekurzivno određivanje determinante, a zatim pozvati funkciju. Promenjena main metoda(funkcija) sada će biti:
#include < stdlib.h >
#include< math.h >
/*Funkcija za ispisivanje matrice
* parametri su
* a- pokazivač na matricu(pokazivač na pokazivač)
* n -dimenzija matrice
*/
void ispisatiMatricu( int ** a, int n)
{
{
{
printf("\n");
int main()
{
int **A;
printf("n=?\n");
scanf("%d",&n);
A=(int**)malloc(n*sizeof(int*));
printf("Matrica?\n");
for(int i=0; i < n; i++)
{
for(int j=0; j < n; j++)
{
printf("Matrica ispis:\n");
ispisatiMatricu(A,n);
for(int i=0; i < n; i++)
{
int * redP = (int*) malloc(n*sizeof(int));
for(int i=0; i < n; i++)
{
int r=0,c=-1,ponovo=1;
while(ponovo)
{
Stavi -1 za red ako je razvijanje po koloni i obrnuto\n",n);
scanf("%d%d",&r,&c);
int d=determinanta(A,n,r,c,n,redP,colP);/*parametri: matrica n*n(A), red po kome ce se razvijati, kolona=-1 znaci da se ne razvija po koloni, niz precrtanih redova, niz precrtanih kolona*/
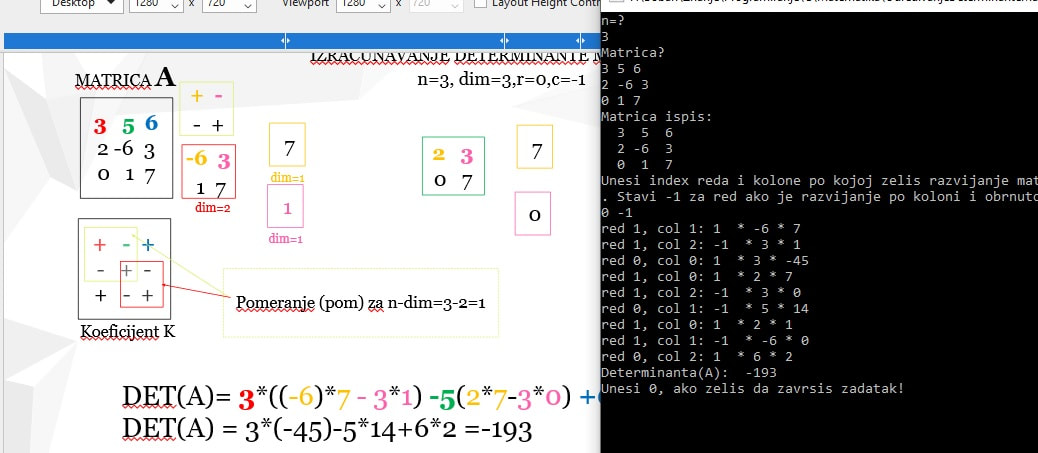
printf("Determinanta(A): %d\n",d);
printf("Unesi 0, ako zelis da zavrsis zadatak!");
scanf("%d",&ponovo);
printf("Kraj\n");
Ovi pokazivači će biti prosleđeni kao parametri u pozivu funkcije za izračunavanje determinante. Takođe se prosleđuju red r i kolona c po kojoj se determinanta razvija. Npr. ako treba da se razvije po prvom redu(indeks i je 0), onda je r=0, a kolona c=-1. Vrednost (-1) govori da se ne razvija po koloni. Ako bi se npr. razvijalo po 2. koloni(j=1), onda bi bilo r=-1, a c=1.
U nastavku je pokazana rekurzivna funkcija determinanta() - postupak, a posle toga i kod.
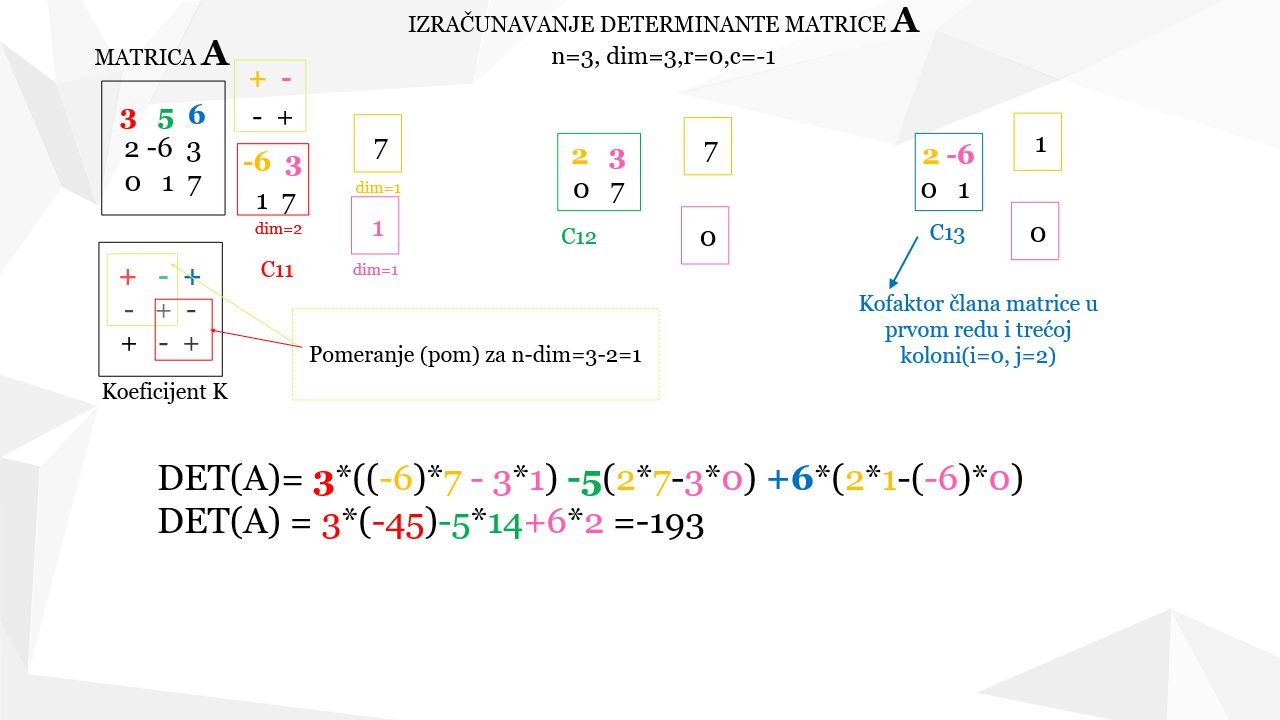
Na slici 2 je prikazan postupak razvijanja matrice dimenzija 3*3 po prvom redu(r=0, c=-1), radi određivanja determinante iste kvadratne matrice.
. Postupak izračunavanja determinante možete pogledati na web strani:Određivanje determinante kvadratne matrice
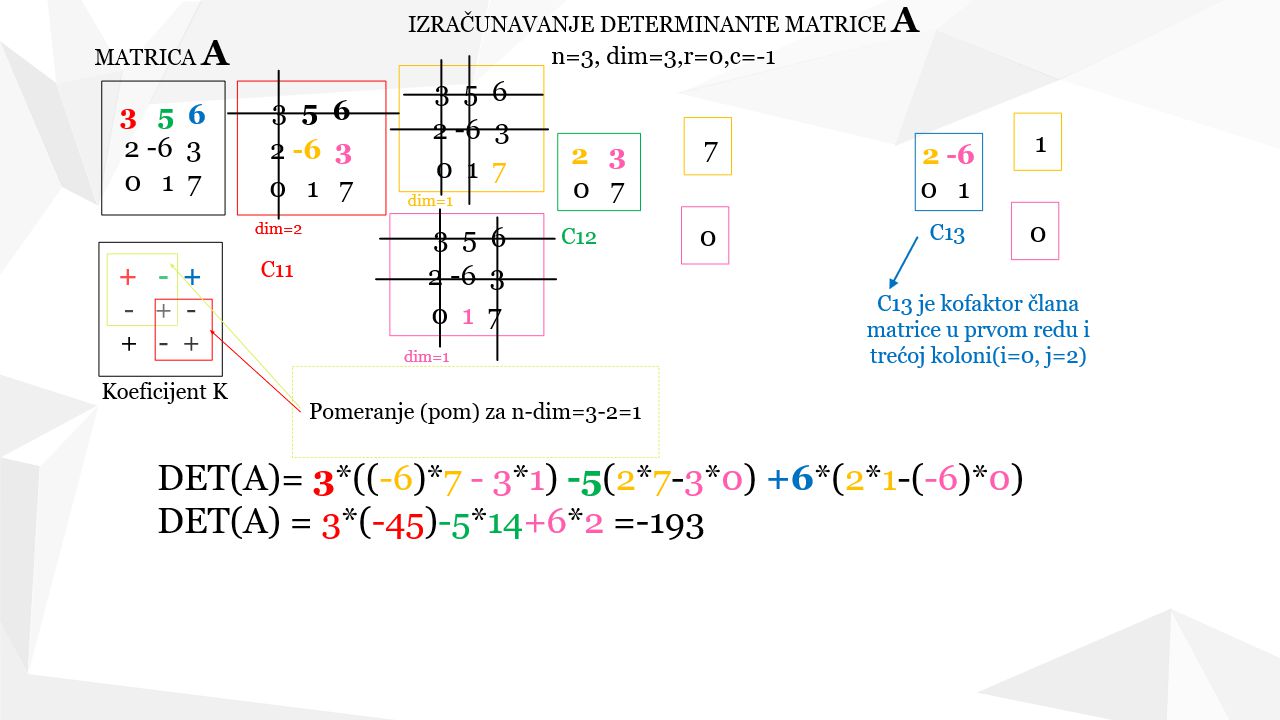
Algoritam je rekurzivan, tj. da bi se odredio kofaktor određenog člana, npr. kofaktor od elementa a11=3(obojeno crvenom bojom na slici), potrebno je odrediti kofaktor C11, koji predstavlja determinantu nižeg reda, u ovom primeru 2*2 i to su elementi [ -6, 3, 1, 7], uokvireni crvenim pravougaonikom na slici . Sada se taj kofaktor tj. determinanta 2*2 takođe razvija po prvoj koloni tj po elementima a11=-6 i a12=3, a odgovarajući kofaktori su sada determinante prvog reda C11= 7 i C12=-1. Pored vrednosti mora se uzeti i koeficijent K= (-1)i+j, gde je i-red, a j-kolona matrice čija se determinanta određuje(vidi tabelu sa "+" i "-", na slici. Tako se za kofaktor C12 dobija -1 jer je koeficijent u prvom redu i prvoj koloni K11=(-1)1+1=-1. Ako bi smo posmatrali početnu tabelu 3*3 sa "+" i "-", onda ne gledamo znak kofaktora u preseku 2. reda i 2. kolone gde se nalazi element matrice -6, nego moramo da se pomerimo, za jedno mesto levo i gore tj. za pom= n-dim=3-2=1, gde je n=3, početna dimenzija matrice, a dim=2 trenutna dimenzija matrice, jer u matrici 3*3 na poziciji člana a22 je koeficijent "-", a zapravo u matrici 2*2 to je pozicija a11, gde je znak "+".
Da bi se izbeglo prepisivanje kofaktora nekog elementa matrice u novu matricu, jer ta operacija, u slučaju velike dimenzije matrice može da zahteva veliki broj operacija, što bi usporilo izvršavanje programa, određivanje kofaktora će biti urađeno na originalnoj matrici, tako što se odgovarajući red ili kolona precrtaju, što je prikazano na sledećoj slici, tj. slici 3:
parametri:
a-matrica početna n*n
n-dimenzija kvadratne matrice
r-red za razvijanje matrice ili -1 ako se ne razvija po redu
c-kolona za razvijanje matrice ili -1 ako se ne razvija po koloni
redP-niz precrtanih redova u matrici
colP-niz precrtanih kolona u matrici
*/
int determinanta(int ** a,int n, int r,int c,int dim, int * redP, int * colP)
{
if(dim==1)
{
while(redP[i])
{
while(colP[j])
{
rez=a[i][j];
else
{
if(r!=-1 && c==-1) //ako se determinanta razvija po redu
{
while(redP[r]){
r=r%n;//korekcija ako je r > n
for(int j = 0,t = 0; j < n; j++)
{
{
k=(int)pow(-1,(r-pom+t));//koeficijent kofaktora(1 ili -1)
colP[j]=1;//precrtana kolona u velikoj matrici
redP[r]=1;//precrtan red u velikoj matrici
/*Rekurzivni poziv iste funkcije*/
int d=determinanta(a,n,0,-1,dim-1,redP,colP);
printf("red %d, col %d: %d * %d * %d\n",r,j,k,a[r][j],d);
rez=rez+k*a[r][j]*d;
colP[j]=0;//vracena precrtana kolona u velikoj matrici
redP[r]=0;//vracen precrtan red u velikoj matrici
t++;
}
else if(c!=-1 && r==-1)
{
while(colP[c]){
c=c%n;//korekcija ako je r>n
for(int i=0,h=0; i < n; i++)
{
{
k=(int)pow(-1,(c-pom+h));//koeficijent kofaktora(1 ili -1)
colP[c]=1;//precrtana kolona u velikoj matrici
redP[i]=1;//precrtan red u velikoj matrici
int d=determinanta(a,n,-1,0,dim-1,redP,colP);
printf("red %d, col %d: %d * %d * %d\n",i,c,k,a[i][c],d);
rez=rez+k*a[i][c]*d;
colP[c]=0;//vracena precrtana kolona u velikoj matrici
redP[i]=0;//vracen precrtan red u velikoj matrici
h++;
else /*Greska*/
{
return -1;
return rez;
Parametar dim je trenutna dimenzija matrice unutar tekuće iteracije u rekurziji i smanjuje se u svakoj sledećoj iteraciji.
Preostala dva parametra redP i colP su pokazivači na nizove tipa bool, gde indeks u nizu odgovara nekom redu tj. koloni, a vrednost, ako je true(1) govori o tome, da je taj red ili kolona precrtan(precrtana). Ovo je je zbog toga da bi se izbeglo da se u svakoj iteraciji odgovarajući kofaktor prepisuje u novu matricu, što bi znatno usporilo izvršavanje programa.
Unutar funkcije razlikujemo dva slučaja, kada je dim = 1 i dim različito od 1. Prvi je zapravo poslednja iteracija, kada se kofaktor svede na matricu dimenzije 1 i tada se vraća vrednost determinante jednaka tom članu matrice, gde se još vodi i računa o predznaku, da li je 1 ili -1.
U drugom delu se razvija matrica, po redu r ili koloni c i vrednost determinante se izračunava pravljenjem izraza sa članovima razvijenog npr. reda i odgovarajućeg kofaktora. Taj kofaktor je nova determinanta koja se dobija od prethodne, dodatnim precrtavanjem reda i kolone u kojoj se nalazi pomenuti član matrice. To znači da se za izračunavanje kofaktora mora ponovo pozvati ista funkcija determinanta(), ali sada sa novim pripremljenim parametrima što se može videti u prikazanom kodu.
Određivanje inverzne matrice
Prethodni opisani kod ćemo sada iskoristiti da odredimo inverznu matricu.
Dodaćemo funkcije adjugovana(int ** a, int n), koja prihvata kao parametre pokazivač na matricu i dimenziju kvadratne matrice n i funkciju float ** inverzna(int ** aT, int det, int n), koja kao parametre prihvata transponovanu matricu, vrednost izračunate determinante učitane matrice A, kao i dimenziju matrice n.
Transponovana matrica i njeno određivanje su objašnjeni u članku: Dvodimenzioni dinamički nizovi-matrice
Određivanje determinante je objašnjeno, prethodno u ovom članku, a ono što je potrebno znati o adjugovanoj matrici možete pročitati u članku: bs.wikipedia.org/wiki/Adjungovana_matrica
U nastavku će biti opisana metoda koja računa adjugovanu matricu.
Adjugovana matrica
{
aA= copyMatrix(a,n);
int k=1;
for(int i=0; i < n; i++)
{
{
for(int i=0; i < n; i++)
{
int * redP=(int*) malloc(n*sizeof(int));
for(int i=0; i < n; i++)
{
redP[i]=1;
colP[j]=1;
int kofA;
kofA=determinanta(aA,n,0,-1,n-1,redP,colP);
k=(int)pow(-1,(i+j));
a[i][j]=k*kofA;
free(redP);
free(colP);
Odgovarajući minor matrice se sada izračunava pozivom prethodno kreirane funkcije za izračunavanje determinante i prosleđivanjem kao parametra: pokazivača na matricu aA, dimenziju n, zatim indekse r= 0 za red, a c=-1 za kolonu, što znači da će se determinanta razvijati po redu sa indeksom 0, tj. prvom redu i na kraju nizove sa logičkim podacima koji govore o tome koji su redovi i kolone precrtani(objašnjeno ranije, za izračunavanje determinante kvadratne matrice).
Unutar main metode treba dodati poziv ove funkcije:
int d=determinanta(A,n,0,-1,n,redP,colP);/*parametri: matrica n*n(A), red po kome ce se razvijati,
kolona=-1 znaci da se ne razvija po koloni, niz precrtanih redova, niz precrtanih kolona*/
free(colP); // oslobađa dinamičku memoriju za colP
free(redP);//
printf("Determinanta(A): %d\n",d);
{
printf("Matrica je singularna");
return 0;
}
transponovana(A,n);
ispisatiMatricu(A,n);
printf("Adjugovana matrica A:\n");
adjugovana(A,n);
ispisatiMatricu(A,n);
U slučaju da je matrica regularna, određuje se prvo adjugovana, a zatim i inverzna matrica(biće prikazano u nastavku).
Funkcija za određivanje inverzne matrice
parametri:
a-matrica početna n*n
n-dimenzija kvadratne matrice
r-red za razvijanje matrice ili -1 ako se ne razvija po redu
c-kolona za razvijanje matrice ili -1 ako se ne razvija po koloni
redP-niz precrtanih redova u matrici
colP-niz precrtanih kolona u matrici
*/
float ** inverzna(int ** aT, int det, int n)
{
aI = (float **)malloc(n*sizeof(float*));
for(int i=0; i < n; i++)
{
for(int j=0; j < n; j++)
{
return aI;
Inverzna matrica aI se određuje tako što se koristeći ugnježdene petlje prolazi kroz elemente adjugovane matrice i ti elementi se zamenjuju količnikom istog elementa i vrednosti determinante d, koja je takođe bila prosleđena kao parametar funkciji.
S obzirom da rezultat deljenja mođe biti i realan broj, ova funkcija vraća pokazivač na pokazivač, ali na float tip podatka.
int d=determinanta(A,n,0,-1,n,redP,colP);/*parametri: matrica n*n(A), red po kome ce se razvijati,
kolona=-1 znaci da se ne razvija po koloni, niz precrtanih redova, niz precrtanih kolona*/
free(colP); // oslobađa dinamičku memoriju za colP
free(redP);//
printf("Determinanta(A): %d\n",d);
if(d==0)
{
return 0;
transponovana(A,n);
ispisatiMatricu(A,n);
printf("Adjugovana matrica A:\n");
adjugovana(A,n);
ispisatiMatricu(A,n);
AI=inverzna(A,d,n);
ispisatiMatricuF(AI,n);
Metoda ispisiMatricuF(AI,n) se poziva za ispisivanje matrice čije su vrednosti podaci tipa float i ona je prikazana u nastavku:
{
{
printf("%.2f ",a[i][j]);
printf("\n");
|
Prethodno
|< Binarna pretraga |
Sledeće
Zamena iteracija formulom >| |