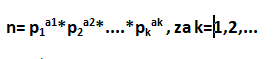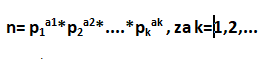THE SIEVE OF ERATOSTHENES ALGORITHM
Eratosthenes sieve is an algorithm that helps to quickly solve the following problem:
For a given natural number, n determine all the prime numbers in the segment of [1, n].
This problem can be solved by passing through the loop in the order of 1-n and checking each number whether it is prime using a function that determines whether to send the number is prime:
For a given natural number, n determine all the prime numbers in the segment of [1, n].
This problem can be solved by passing through the loop in the order of 1-n and checking each number whether it is prime using a function that determines whether to send the number is prime:
bool isPrime(long long n)
{
if(n==1)
return false;
long long d=2;
while(d*d<=n) {
if(n % d == 0)
{
return false;
}
d=d+1;
}
return true;
}
{
if(n==1)
return false;
long long d=2;
while(d*d<=n) {
if(n % d == 0)
{
return false;
}
d=d+1;
}
return true;
}
Therefore, the main function would be:
int main()
{
int n;
cin >> n;
for(int i=1;i<=n;i++)
{
if(isPrime(i)){
cout << i << endl;
}
}
return 0;
}
{
int n;
cin >> n;
for(int i=1;i<=n;i++)
{
if(isPrime(i)){
cout << i << endl;
}
}
return 0;
}
|
This method would be too slow for a lot of n, because it checks all the numbers in a row.
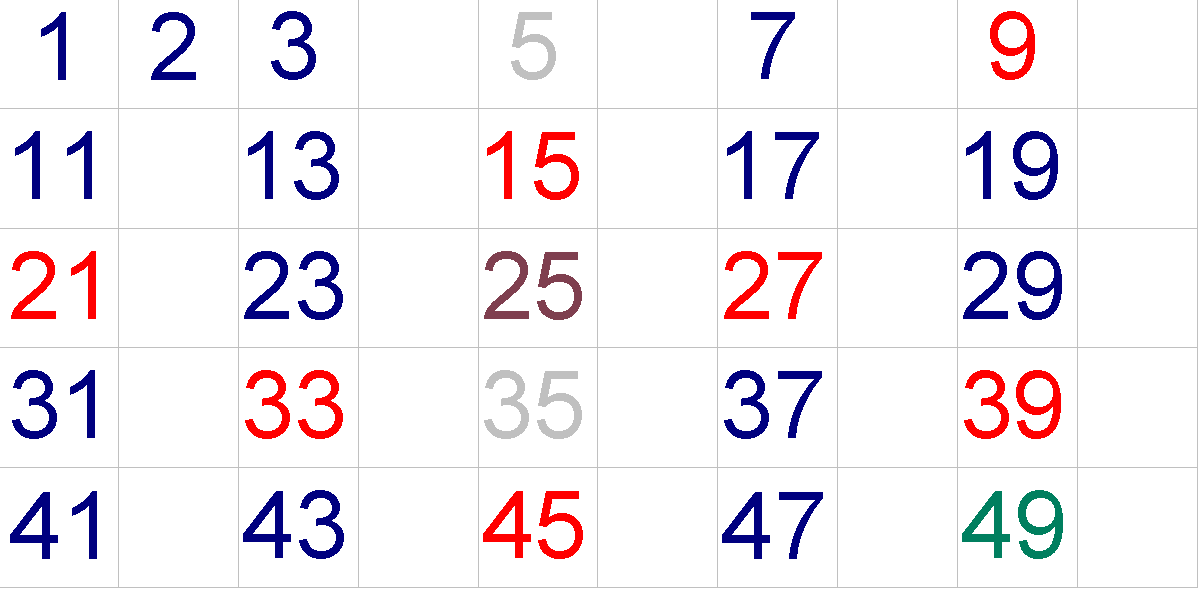
This can be accelerated a little if instead of examining the numbers in the order of 1 to n^1/2, we end up with a number that will slightly accelerate the algorithm. We will get real acceleration with the Eratosthenes sieve. Algorithm Eratosthenes sieve: It is based on the idea that in one pass we check more numbers at once. Assume that n = 50, i.e. that all numbers between 1 and 50 should be checked if they are prime: |
|
Let's take the first potential divisor of number 50, which is surely a simple number, and remove from the sequence all the numbers that are shared with this potential sniper. This is number 2. The numbers from the array are folded because they are certainly not prime numbers, because they are divisible by 2, except with 1 and with itself. This could be solved by a loop in which the current variable changes from 2 to 50 ^ 1/2 ~ 7.07 ~ 7. So the last prime number to be divisor is 7. After removing numbers divisible by 2, the state is as follows:
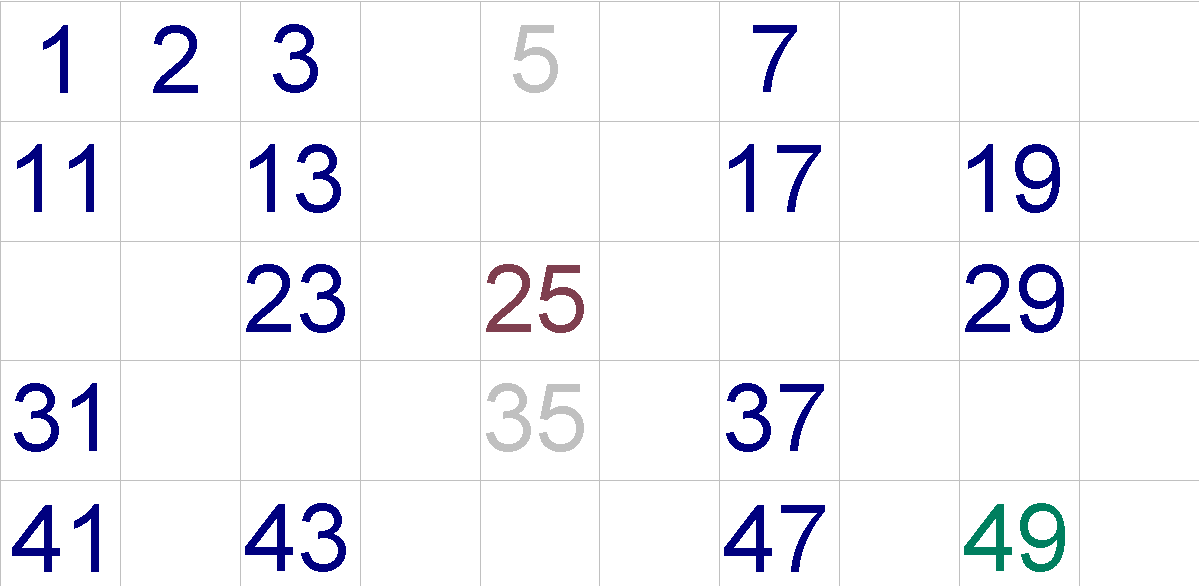
This procedure is repeated with the next number which is not removed . If the number has not been removed previously, this means that it is prime. So we will now remove all numbers that are greater than 3 and are shared with 3. After that, it will remain:
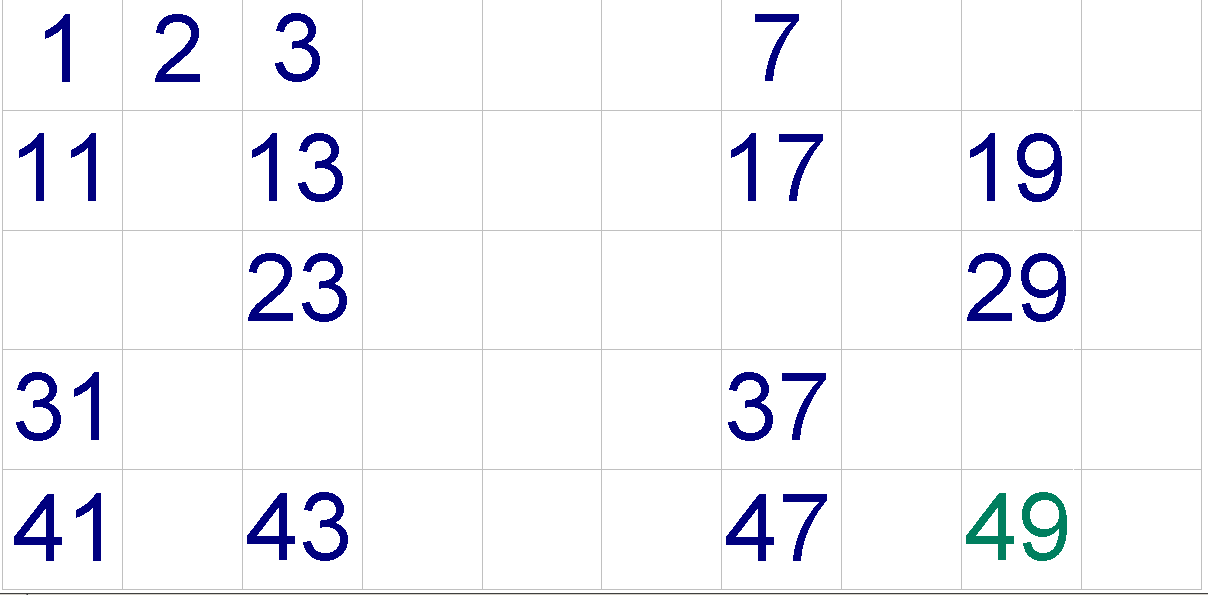
So we will now remove all numbers that are greater than 5 and are divisible by 5. After that, it will remain:
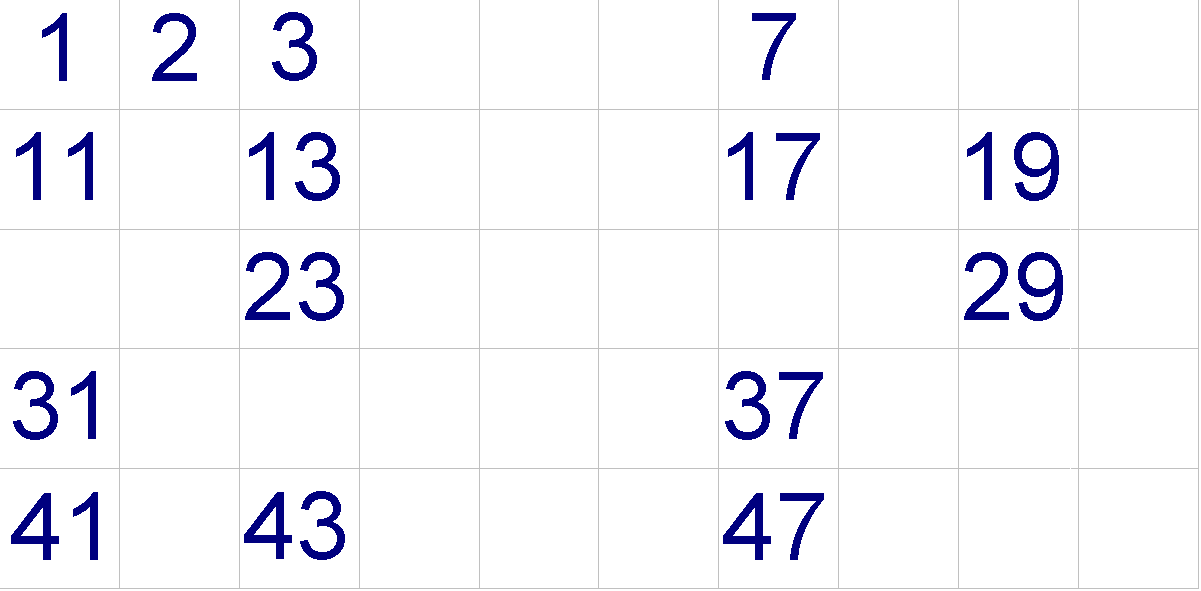
It remains to remove all numbers that are larger than 7 and which are divisible by 7. That's in this case only number 49. After that, it will remain:
The numbers remaining are prime numbers.
The Sieve of Eratosthenes - cod
The function that removes these (not prime) numbers would look like:
void eratosten(int n)
{
for(int i=2; i < sqrt(n); i++)
{
if(P[i])
{
for(int j=i; j < n/i; j++)
{
P[i*j]=false;
}
}
}
}
{
for(int i=2; i < sqrt(n); i++)
{
if(P[i])
{
for(int j=i; j < n/i; j++)
{
P[i*j]=false;
}
}
}
}
The current element in the loop is a delimiter for which we verify that the numbers that are potentially need to be removed are divisible by itself. Remembering the remaining numbers is done using the sequence P. First, we check whether the number that is a potential divisor is still in sequence. If he is, he is a divisor with whom we will remove his content. If not, then this number can not be a divisor because it is not prime.
If it is a divisor, then we perform a check through the loop for numbers starting from the squares of the sender. The x numbers between the divisor and the squares of the divisor (i <x <i * i) have already been checked by the previous divisor and should not be checked. The number of numbers to be removed is obtained as n / i - i. In the previous example, where n = 50, and the divisor 2 it would be 50 / 2 - 2 = 25-2 = 23. This is logical because it has 25 natural numbers that are divisible from 2 to 50, and since we exclude 1 i 2, 23 numbers remain.
We remove the numbers by placing a member of a array at a position equal to the number that is removed to false. After repeating the procedure with all sorts, the sequence will remain true at the position of the prime numbers. Of course, before this procedure, the entire set of P must be initialized. The main method would be:
If it is a divisor, then we perform a check through the loop for numbers starting from the squares of the sender. The x numbers between the divisor and the squares of the divisor (i <x <i * i) have already been checked by the previous divisor and should not be checked. The number of numbers to be removed is obtained as n / i - i. In the previous example, where n = 50, and the divisor 2 it would be 50 / 2 - 2 = 25-2 = 23. This is logical because it has 25 natural numbers that are divisible from 2 to 50, and since we exclude 1 i 2, 23 numbers remain.
We remove the numbers by placing a member of a array at a position equal to the number that is removed to false. After repeating the procedure with all sorts, the sequence will remain true at the position of the prime numbers. Of course, before this procedure, the entire set of P must be initialized. The main method would be:
int main()
{
int n;
cin >> n;
for(int i = 1;i < n;i++) {
P[i]=true;
}
eratosten(n);
for(int i = 1; i <= n; i++)
{
if(P[i])
cout << i << endl;
}
return 0;
}
{
int n;
cin >> n;
for(int i = 1;i < n;i++) {
P[i]=true;
}
eratosten(n);
for(int i = 1; i <= n; i++)
{
if(P[i])
cout << i << endl;
}
return 0;
}
You should add in the code above the method:
#include
#define DIM 1000
using namespace std;
bool P[DIM+1];
#define DIM 1000
using namespace std;
bool P[DIM+1];
Use of Eratosthenes sieve for Factoring
In order to factor a number n, that is, to split into simple factors, we need to know all the simple factors even if they multiply pk and then the number n can be written in the following form:
Eg. if n = 50
Using the Sieve of Eratosthenes algorithm, we can first determine p1, p2, ... pk, i.e. dividers.
Then, the number n is first divisible by p1, repeating the division as long as the remainder is partitioned with p1, so the further division process is repeated with p2, etc.
Let's look at the example shown at the beginning, for n = 50. In order to factor this factor, we should begin to share this number with its smallest divisor, which is in this case number 2 and repeat the procedure as long as the remainder of the division is still divisible by 2.
1 cycle: 50/2 = 25, the rest is 25
Number 25 can not bi divided by 2 furthermore.
Next, the procedure repeats with the rest, which is number 25 and its smallest divider is 5:
1 cycle: 25/5 = 5, the rest is 5
2 cycles: 5/5 = 1, the remainder is 1
Here the process ends.
We can use the sieve of Eratosthenes algorithm here to determine for each number x its smallest divisor instead of removing it. In the example shown, these would be numbers 2 and 5.
Next, the cycle separation process shown would be done using the loop.
At the beginning, first prepare the arrays:
Then, the number n is first divisible by p1, repeating the division as long as the remainder is partitioned with p1, so the further division process is repeated with p2, etc.
Let's look at the example shown at the beginning, for n = 50. In order to factor this factor, we should begin to share this number with its smallest divisor, which is in this case number 2 and repeat the procedure as long as the remainder of the division is still divisible by 2.
1 cycle: 50/2 = 25, the rest is 25
Number 25 can not bi divided by 2 furthermore.
Next, the procedure repeats with the rest, which is number 25 and its smallest divider is 5:
1 cycle: 25/5 = 5, the rest is 5
2 cycles: 5/5 = 1, the remainder is 1
Here the process ends.
We can use the sieve of Eratosthenes algorithm here to determine for each number x its smallest divisor instead of removing it. In the example shown, these would be numbers 2 and 5.
Next, the cycle separation process shown would be done using the loop.
At the beginning, first prepare the arrays:
#include < iostream >
using namespace std;
#include< math.h >
#define DIM 1000
using namespace std;
int D[DIM+1];
int a[DIM+1];
int p[DIM+1];
using namespace std;
#include< math.h >
#define DIM 1000
using namespace std;
int D[DIM+1];
int a[DIM+1];
int p[DIM+1];
A function that determines the least divisor of numbers:
void eratosten(int n)
{
for(int i = 1; i <= n; i++)
{
D[i]=i;
}
for(int i = 2; i < sqrt(n); i++)
{
if(D[i]==i)
{
for(int j = i; j <= n/i; j++)
{
/*Search for a smaller number divider "(i*j)" i "i"*/
if(D[i] < D[i*j]) /*If the number of the tested number is smaller than the divisor of his own divisor*/
D[i*j]=D[i];
}
}
}
}
{
for(int i = 1; i <= n; i++)
{
D[i]=i;
}
for(int i = 2; i < sqrt(n); i++)
{
if(D[i]==i)
{
for(int j = i; j <= n/i; j++)
{
/*Search for a smaller number divider "(i*j)" i "i"*/
if(D[i] < D[i*j]) /*If the number of the tested number is smaller than the divisor of his own divisor*/
D[i*j]=D[i];
}
}
}
}
In the first loop, he set up the shareholders for all the numbers to be themselves (numbers are shared with oneself). This will remain the smallest particle if it is for free numbers.
Next, for numbers 2 to 2/2, we look at the order of their least divisors. For complex numbers, one that was abolished in their case by their smallest sender, this is the smallest particle, and for the number (i * j). For example, for the number 8, the smallest particle is 2, and the number 8 in the loop is given as 2 * 4, so i = 2, j = 4. In the starting sequence D [8] = 8, D [2] = 2 and after testing conditions if (D [2] <D [2 * 4]) ... the new value D [8] = 2, and the smallest is its divisor.
Now that we know all the smallest dividers, factoring can be done:
Next, for numbers 2 to 2/2, we look at the order of their least divisors. For complex numbers, one that was abolished in their case by their smallest sender, this is the smallest particle, and for the number (i * j). For example, for the number 8, the smallest particle is 2, and the number 8 in the loop is given as 2 * 4, so i = 2, j = 4. In the starting sequence D [8] = 8, D [2] = 2 and after testing conditions if (D [2] <D [2 * 4]) ... the new value D [8] = 2, and the smallest is its divisor.
Now that we know all the smallest dividers, factoring can be done:
int faktoring(int x)
{
int k=0;
while(x > 1)
{
k=k+1;
p[k]=D[x];
a[k]=0;
while(x%p[k]==0)/*Dividing by the smallest divisor while it is possible*/
{
x=x/p[k];
a[k]=a[k]+1;
}
}
return k;
}
{
int k=0;
while(x > 1)
{
k=k+1;
p[k]=D[x];
a[k]=0;
while(x%p[k]==0)/*Dividing by the smallest divisor while it is possible*/
{
x=x/p[k];
a[k]=a[k]+1;
}
}
return k;
}
|
The elements of the array p are in the order of the smallest the dividers of that number k to be factorized. In the first iteration of the outer loop, the loop is the initial number k, the second is the remainder of the division that remains after dividing with the smallest divisor through the inner loop length. The process is repeated until it reaches 1.
The use of the sieve of Eratosthenes for factoring is used when we have many numbers to be factorized. For example, if the starting number is to be counted, if all numbers of 2-n are to be factorized, this method is suitable. The main method to do this is: |
|
int main()
{
int n,k;
cin >> n;
eratosten(n);
for(int i = 2; i <= n; i++)
{
k=faktoring(i);
for(int j = 1; j <= k; j++)
{
cout << i << "= " << p[j] << "^" << a[j];
if(j != k)
cout << "*";
else
cout << ";";
}
cout << endl;
}
return 0;
}
{
int n,k;
cin >> n;
eratosten(n);
for(int i = 2; i <= n; i++)
{
k=faktoring(i);
for(int j = 1; j <= k; j++)
{
cout << i << "= " << p[j] << "^" << a[j];
if(j != k)
cout << "*";
else
cout << ";";
}
cout << endl;
}
return 0;
}
|
Previous
|< A prime numbers and factoring |